Терминология
Часто под CRC подразумевают две разные вещи:
Cyclic Redundancy Code — применяется в помехоустойчивом кодировании для обнаружения и исправления ошибок
Cyclic Redundancy Check — использование циклических кодов в качестве хэш-функции для проверки целостности принимаемых даных
Поскольку большинство современных проводных каналов связи обладают достаточными характеристиками для поддержания хорошего BER, то зачастую достаточно убедиться в том, что сообщение не искажено во время прохождения по внешнему каналу, а для этого достаточно использования циклических кодов в качестве контрольных сумм (перезапрос «бракованного» кадра как правило в большинстве интерфейсов происходит на более высоком протокольном уровне).
Критерии качества
Качественным критерием оценки контрольной суммы является вероятность возникновения коллизии — т.е. необнаружения искажения данных: подразумевается искажение данных таким образом, что подсчитанный CRC (от искаженных данных) совпадет с референсным CRC (либо одновременно исказятся и CRC и данные в канале передачи). Причём, чем длиннее сообщение, тем больше вероятность появления коллизии — больше возможностей для того чтобы «звёзды совпали», поэтому часто выбор длины полинома для подсчёта CRC соотносят с размером пакета, к которому этот CRC применяют.
Для этого ввели такой термин как Расстояние Хэмминга (Hamming Distance, HD) или Метрика Минковского — она служит некоей метрикой различности двух объектов (в нашем случае — двух пакетов: переданного и принятого). В терминах CRC, HD — это минимально возможное число бит сообщения, инверсия которых может привести к коллизии (необнаружению повреждения сообщения). Так, например в стандарте CAN (от Bosch GmbH) используемый полином вкупе с длиной сообщений обеспечивает HD=6, что означает, что не существует никаких комбинаций 1-, 2-, 3-, 4- и 5-битных ошибок (здесь ошибка — инверсия передаваемого бита в сообщении), которые не были бы необнаруживаемыми, но существует как минимум одна комбинация 6-ти битной ошибки, которую невозможно обнаружить с помощью используемого полинома CRC.
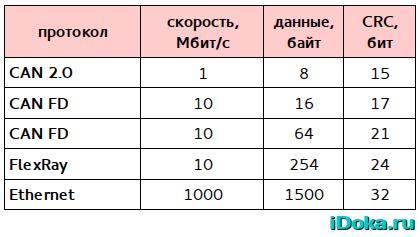
Также необходимо отметить, что на правильность выбора полинома для того или иного протокола (и получения конкретного значения HD) зависит и скорость передачи информации — характер ошибок и их динамика может сильно меняться (например, за счет увеличения скорости передачи — появляться пачки ошибок), вот для примера какие цифры фигурируют в знакомых мне протоколах:
Дань традициям
В большинстве стандартизированных протоколов используются контрольные суммы CRC, однако часто используемые в них стандартизованные полиномы не являются самыми эффективными в терминах эффективного расстояния Хэмминга (HD), в [1] затрагивается вопрос на всю глубину: большинство стандартов в плане обнаружения ошибок не столь эффективны, как могли бы быть, из-за того, что используется полином для контрольной суммы, однажды выбранный на этапе утверждения стандарта.
Наиболее яркий пример — стандарт на Ethernet-пакеты IEEE 802.3, который использует самый популярный 32-разрядный полином, но в то же время, использование иных 32-разрядных полиномов (CRC32C, CRC32K, etc) позволило бы достичь лучших показателей (в терминах HD) в различных диапазонах длин передаваемых сообщений, посмотрим на таблицу:
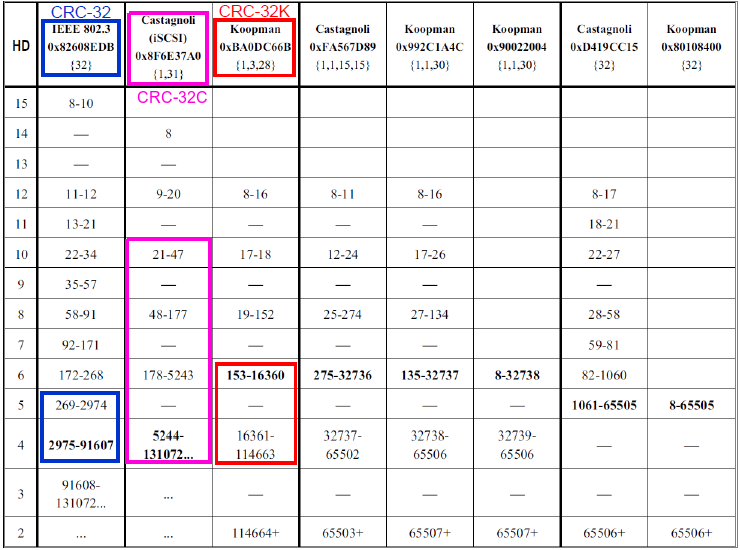
Видно, что стандартный полином CRC32 на пакетах свыше 372 байт имеет HD=4, в то время как CRC32K на пакетах до 2045 байт имеет HD=6, А если оперировать Jumbo-фреймами, то CRC32C на пакетах до 16 КБайт обеспечивает HD=4 (в то время как стандартный CRC32 обеспечивает HD=4 при длине пакета до 11,5 КБайт). Т.о. видно, что если есть возможность отойти от стандарта (например, создание своего полностью кастомного оборудования для стандартных протоколов, которое работает только во внутренней собственной инфраструктуре) следует воспользоваться этой возможностью — в случае стандартного Ethernet можно сделать модификацию под какой-нибудь Industrial Ethernet с CRC32C/CRC32K, снизив вероятность необнаружения ошибки или увеличив размер пакета по отношению к стандартному, не снижая при этом имеющегося HD.
Мораль
Не только при конструировании новых протоколов обмена, но и при реализации стандартных полезно сверяться прежде всего не со стандартами, а с работами, подобными Best CRC Polynomials, особенно если специфике вашей работы свойственно выжимать максимум из возможного и где цена необнаружения ошибки высока (Aerospace/Aircraft, Industrial, Automotive).
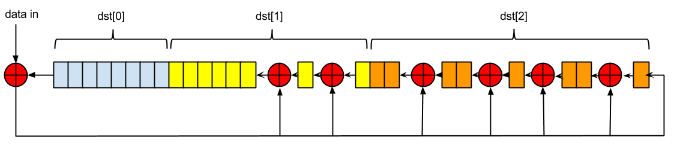
Следующим призывом будет там где это возможно писать на верилоге модули CRC, конфигурируемые не параметрами, а в процессе работы (on-the-fly). Это легко реализуется (в первую очередь — с минимальными аппаратными затратами), если вычислять CRC через последовательную реализацию (LFSR), а не по 4/8/N-бит за такт.
Тест на внимательность
В заголовке статьи использована картинка с LFSR, реализующим 24-битный CRC на verilog (из BLE), а не CRC32 из IEEE 802.3 как могло показаться.
Литература
Philip Koopman, Cyclic Redundancy Code (CRC) Polynomial Selection For Embedded Networks
Блейхут Ричард. Теория и практика кодов, контролирующих ошибки [Theory and Practice of Error Control Codes] — М.: Мир, 1986.
Richard W. Hamming. Error-detecting and error-correcting codes, Bell System Technical Journal 29(2):147-160, 1950.